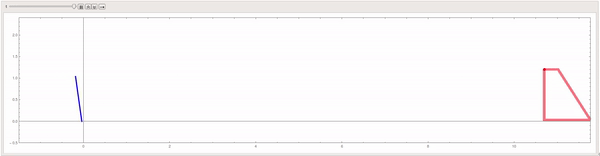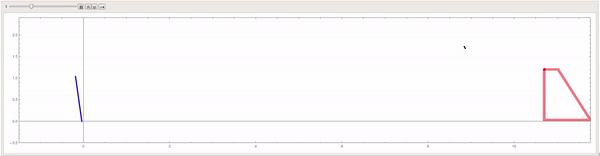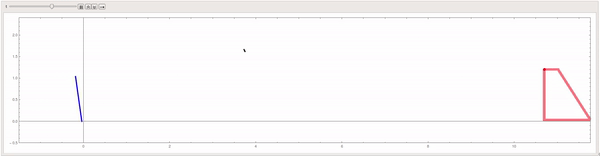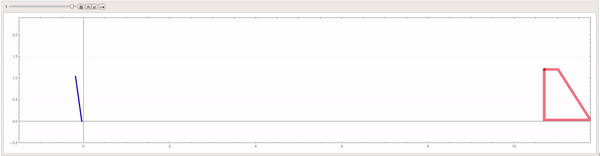
Mathematica simulation of a hockey puck hitting the crossbar of a goal.
Description
The goal of this project was to simulate a hockey stick striking a puck at an angle and having the puck hit the crossbar of a goal. The simulation models the system from the side. From this view, there is a hockey stick, a puck, and a goal. The hockey stick is modeled as a pendulum which has an external force acting on it to simulate a player swinging a real hockey stick. The puck is a rectangle from the side view and thus has rotational and translational kinetic energy upon being hit and hitting the crossbar. In reality, the flex of a hockey stick upon impact with the puck would cause the puck to gain the lift necessary for it to travel from ice-level to the height of the crossbar. To simplify things in this simulation, the puck has an initial angle necessary to cover that vertical distance. The crossbar itself is a cylindrical object which viewed from the side is a circle.
Euler-Lagrange Equations
This dynamic system was modeled using the Euler-Lagrange method which was calculated using the kinetic energy and potential energy of both the stick and the puck. For both I used the twist matrix (V) and the inertia matrix (Itot) to calculate kinetic energy and I used the mass of each and their vertical positions (y) to calculate potential energy.
Constraints
There are two impacts in the system: one in which the hockey stick strikes the puck and another in which the hockey puck strikes the crossbar. For the first impact, I attempted to model my constraint as point at which the front edge of the hockey stick meets the rear edge of the puck. For the second impact, I used the point at which the front edge of the puck meets the x-location of the front of the crossbar as my constraint.
External Forces
The hockey stick has a constant force applied of 243.5N. This force was chosen to create a tangential velocity of 100mph (44.704m/s) at the end of the stick when it contacts the puck.